Phage One-Step Growth Case Study#
This example uses the model developed in the paper: https://www.biorxiv.org/content/10.1101/2025.05.15.651590v1
A compartmental model of ODE is used in this example, where the bacterial cells goes through different stages of infection. They are given by Susceptible (S), Exposed (E), Infected (I), and the free virus is given by (V). The model is parameterized by traits such as \(r,\phi,\tau,\beta\), the bacterial growth rate, adsorption rate, latent period and burst size respectively. For more information please consult the paper. Here is the differential equation.
\[\frac{dS}{dt} = rS - \phi SV\]
\[\frac{dE_1}{dt} = \phi SV - \frac{N_E+1}{\tau}E_1\]
\[\frac{dE_i}{dt} = \frac{N_E+1}{\tau}E_{i-1} - \frac{N_E+1}{\tau}E_{i}\]
\[\frac{dE_{N_E}}{dt} = \frac{N_E+1}{\tau}E_{N_E-1} - \frac{N_E+1}{\tau}E_{N_E}\]
\[\frac{dI}{dt} = \frac{N_E+1}{\tau}E_{N_E} - \frac{N_E+1}{\tau}I\]
\[\frac{dV}{dt} = \beta\frac{N_E+1}{\tau}I - V\phi (S+\sum E_i + I)\]
Here only \(V\) is observed.
[1]:
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import os
import sys
import scipy.io
from concurrent.futures import ProcessPoolExecutor
# Get path
project_root = os.path.abspath(os.path.join(os.getcwd(), '..','..','..'))
sys.path.insert(0, project_root)
[2]:
import sys
sys.path.append('./..') # or absolute path if needed
from invode import ODEOptimizer, lhs_sample, load_matlab_data
[3]:
'''
file_path = './../sample_data/HS6_13-15_2024.mat'
free_phages = load_matlab_data(file_path)['free_phages']
S0 = np.mean(load_matlab_data(file_path)['S0_replicates'])
V0 = np.mean(load_matlab_data(file_path)['V0_replicates'])
time = load_matlab_data(file_path)['time_free_phages'].flatten()/60 # Convert time to hours
'''
free_phages = np.array([[ 13200, 13500, 15400],
[ 15500, 11800, 14450],
[ 17200, 13100, 15000],
[ 12100, 13000, 14500],
[ 16700, 12900, 13500],
[ 194000, 60000, 67000],
[ 2860000, 1280000, 1410000],
[12200000, 11100000, 10100000],
[42000000, 27300000, 25350000],
[49000000, 53000000, 47000000],
[58500000, 50500000, 61000000],
[42500000, 33000000, 44000000]])
time = np.array([0. , 0.33333333, 0.66666667, 1. , 1.16666667,
1.33333333, 1.5 , 1.66666667, 1.83333333, 2. ,
2.33333333, 2.66666667])
S0 = 128906002
V0 = np.mean(free_phages[:,0])
We can have a initial guess if we want to, but not needed. If that is a good candidate, InvODE will also consider it.
[4]:
# Initial guess for parameters ===
initial_guess = {
'r': 0.3,
'phi': 4.5e-08 ,
'beta': 256,
'tau': 2,
'NE': 180
}
# Initial conditions ===
y0 = np.zeros((initial_guess['NE']+3,))
y0[0] = S0
y0[-1] = V0
[5]:
def onstep(y, t, params):
phi = params['phi']
beta = params['beta']
tau = params['tau']
r = params['r']
NE = params['NE']
S = y[0]
E_mat = y[1:NE+1]
I = y[NE+1]
V = y[NE+2]
etaeff = ((NE+1)/tau)
dotS = r*S - phi*V*S
dotE1 = phi*S*V - etaeff * E_mat[0]
if NE > 1:
dotE_mat = np.zeros(NE-1)
dotE_mat[:] = etaeff * E_mat[0:-1] - etaeff * E_mat[1:]
dotI = etaeff * (E_mat[-1] - I)
dotV = beta * etaeff * I - V * phi * (S + I + np.sum(E_mat))
# Build the full derivative vector (same length as y)
dydt = np.zeros_like(y)
dydt[0] = dotS
dydt[1:NE+1] = dotE1 if NE == 1 else np.concatenate([[dotE1], dotE_mat])
dydt[NE+1] = dotI
dydt[NE+2] = dotV
return dydt
[6]:
def simulate_model(params):
# Initial conditions ===
params['NE'] = int(params['NE'])
y0 = np.zeros((params['NE']+3,))
y0[0] = S0
y0[-1] = V0
## dilution step
time_dil = np.linspace(0, 0.25, 200) # Short time for dilution step
sol_dil = odeint(onstep, y0, time_dil, args=(params,))
y0_dil = sol_dil[-1, :]/100 # Use the last state as the new initial condition
## main simulation
sol = odeint(onstep, y0_dil, time, args=(params,))
phage_solution = sol[:,-1]
return phage_solution
[7]:
def mse(model_output):
target = np.mean(free_phages, axis=1)
if len(model_output) != len(target):
raise ValueError("Length mismatch between model output and data")
return np.mean((np.log10(model_output) - np.log10(target)) ** 2)
[8]:
#free_phages_sol = simulate_model(initial_guess)
[9]:
param_bounds = {
'r': 0.3, # fixed
'phi': (1e-8, 1e-7),
'beta': (100, 500),
'tau': (1, 5),
'NE': (100, 200)
}
optimizer = ODEOptimizer(
ode_func=simulate_model,
error_func=mse,
param_bounds=param_bounds,
#initial_guess=initial_guess,
seed=42,
num_top_candidates=2,
n_samples=100,
num_iter=5,
verbose_plot=True,
verbose = True
)
[10]:
optimizer.fit()
Fitting Progress: 0%| | 0/5 [00:00<?, ?it/s]
Iteration 1/5
Fitting Progress: 20%|██████████▏ | 1/5 [00:00<00:03, 1.02it/s]
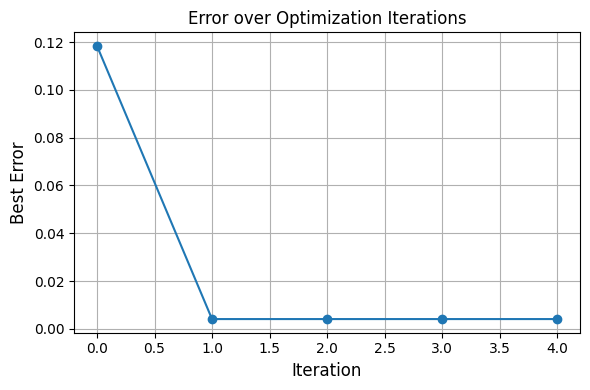
Best error so far: 0.1183
Best params: {'phi': 4.266983966023513e-08, 'beta': 377.39952281604735, 'tau': 2.0208683819873485, 'NE': 157, 'r': 0.3}
Iteration 2/5
Fitting Progress: 40%|████████████████████▍ | 2/5 [00:03<00:05, 1.96s/it]
Best error so far: 0.0041
Best params: {'phi': 7.00989772815266e-08, 'beta': 391.1287225045886, 'tau': 1.9741647732052143, 'NE': 163, 'r': 0.3}
Iteration 3/5
Fitting Progress: 60%|██████████████████████████████▌ | 3/5 [00:06<00:04, 2.39s/it]
Best error so far: 0.0041
Best params: {'phi': 7.00989772815266e-08, 'beta': 391.1287225045886, 'tau': 1.9741647732052143, 'NE': 163, 'r': 0.3}
Iteration 4/5
Fitting Progress: 80%|████████████████████████████████████████▊ | 4/5 [00:09<00:02, 2.56s/it]
Best error so far: 0.0041
Best params: {'phi': 7.00989772815266e-08, 'beta': 391.1287225045886, 'tau': 1.9741647732052143, 'NE': 163, 'r': 0.3}
Iteration 5/5
Fitting Progress: 100%|███████████████████████████████████████████████████| 5/5 [00:12<00:00, 2.43s/it]
Best error so far: 0.0041
Best params: {'phi': 7.00989772815266e-08, 'beta': 391.1287225045886, 'tau': 1.9741647732052143, 'NE': 163, 'r': 0.3}
Refining params: {'phi': 7.013988205829579e-08, 'beta': 348.49148227932295, 'tau': 1.9239617327028835, 'NE': 173}
[Local Optimization]
Refined parameters: {'phi': 6.823759283454945e-08, 'beta': 348.4914781187379, 'tau': 1.9422442211934774, 'NE': 173.0, 'r': 0.3}
Refined error: 0.004188937021152051
Refining params: {'phi': 7.158050791552344e-08, 'beta': 445.2424565642069, 'tau': 1.9461328394135549, 'NE': 154}
[Local Optimization]
Local optimization failed: ABNORMAL_TERMINATION_IN_LNSRCH
After local refinement:
Best params: {'phi': 6.823759283454945e-08, 'beta': 348.4914781187379, 'tau': 1.9422442211934774, 'NE': 173.0, 'r': 0.3}
Best error: 0.0042
[10]:
({'phi': 6.823759283454945e-08,
'beta': 348.4914781187379,
'tau': 1.9422442211934774,
'NE': 173.0,
'r': 0.3},
0.004188937021152051)
[11]:
best_params = optimizer.best_params
[12]:
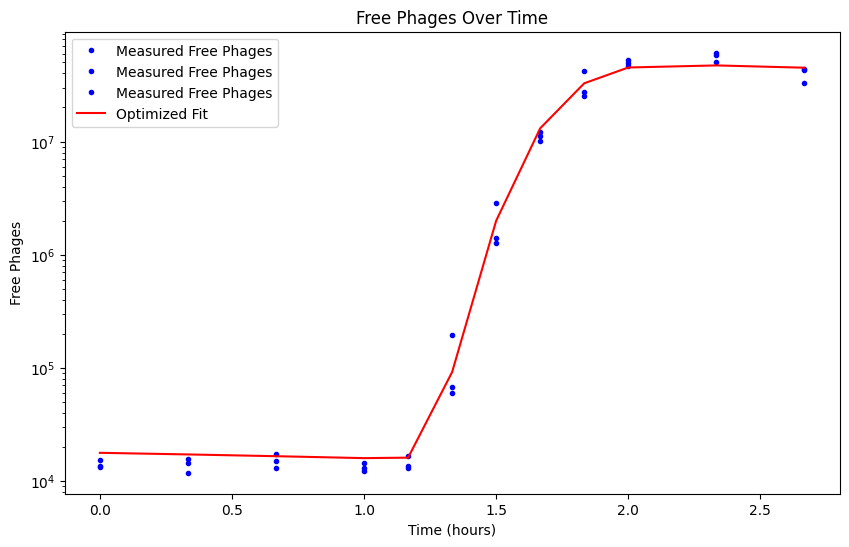
phages_fit = simulate_model(best_params)
plt.figure(figsize=(10, 6))
plt.plot(time, free_phages, label='Measured Free Phages', color='blue', marker='o', markersize=3, linestyle='none')
#plt.plot(time, free_phages_sol, label='Initial Guess', linestyle='--', color='orange')
plt.plot(time, phages_fit, label='Optimized Fit', color='red')
plt.xlabel('Time (hours)')
plt.ylabel('Free Phages')
plt.yscale('log')
plt.title('Free Phages Over Time')
plt.legend()
plt.show()
[13]:
optimizer.summary()
🔍 ODEOptimizer Summary:
ode_func: simulate_model
error_func: mse
param_bounds: {'phi': (1e-08, 1e-07), 'beta': (100, 500), 'tau': (1, 5), 'NE': (100, 200)}
initial_guess: {'phi': 5.4999999999999996e-08, 'beta': 300.0, 'tau': 3.0, 'NE': 150.0, 'r': 0.3}
n_samples: 100
num_iter: 5
num_top_candidates: 2
do_local_opt: True
local_method: L-BFGS-B
shrink_rate: 0.5
parallel: False
local_parallel: False
verbose: True
verbose_plot: True
seed: 42
best_error: 0.004188937021152051
best_params: {'phi': 6.823759283454945e-08, 'beta': 348.4914781187379, 'tau': 1.9422442211934774, 'NE': 173, 'r': 0.3}
[14]:
df = optimizer.get_top_candidates_table()
print(df)
iteration rank error phi beta tau NE r
0 1 1 0.118342 4.266984e-08 377.399523 2.020868 157 0.3
1 1 2 0.131130 4.917636e-08 334.668375 2.045617 168 0.3
2 2 1 0.004130 7.009898e-08 391.128723 1.974165 163 0.3
3 2 2 0.006739 6.835375e-08 294.076868 1.907686 190 0.3
4 3 1 0.005034 7.649504e-08 442.555402 1.990015 153 0.3
5 3 2 0.014846 8.143537e-08 292.647566 1.947413 182 0.3
6 4 1 0.016187 6.538001e-08 242.538774 1.912211 168 0.3
7 4 2 0.020552 8.440974e-08 361.452366 1.934187 158 0.3
8 5 1 0.005695 7.013988e-08 348.491482 1.923962 173 0.3
9 5 2 0.014288 7.158051e-08 445.242457 1.946133 154 0.3
[ ]: