Adding constraints

We again consider the same problem.

\[\frac{dy}{dt} = A\sin(\omega t + \delta)\]

### Dataset
import numpy as np

data = {'Time': np.array([ 0.        ,  0.20408163,  0.40816327,  0.6122449 ,  0.81632653,
        1.02040816,  1.2244898 ,  1.42857143,  1.63265306,  1.83673469,
        2.04081633,  2.24489796,  2.44897959,  2.65306122,  2.85714286,
        3.06122449,  3.26530612,  3.46938776,  3.67346939,  3.87755102,
        4.08163265,  4.28571429,  4.48979592,  4.69387755,  4.89795918,
        5.10204082,  5.30612245,  5.51020408,  5.71428571,  5.91836735,
        6.12244898,  6.32653061,  6.53061224,  6.73469388,  6.93877551,
        7.14285714,  7.34693878,  7.55102041,  7.75510204,  7.95918367,
        8.16326531,  8.36734694,  8.57142857,  8.7755102 ,  8.97959184,
        9.18367347,  9.3877551 ,  9.59183673,  9.79591837, 10.        ]), 'y': np.array([0.91963291, 0.99361406, 1.27816619, 1.83477302, 2.0436977 ,
       2.4108738 , 2.84511313, 2.98244074, 3.01343352, 2.81703372,
       2.66941941, 2.31326251, 1.89208529, 1.40799057, 1.2468084 ,
       1.08452949, 1.03682804, 1.22276976, 1.58095538, 1.73274129,
       2.41068701, 2.6162268 , 3.08196062, 3.0313903 , 2.77556916,
       2.75105715, 2.46021415, 1.85709704, 1.60617448, 1.22300332,
       1.03747336, 1.20756063, 1.10867505, 1.42444299, 1.68301796,
       2.09068759, 2.61731029, 2.42544506, 2.97204288, 2.97302454,
       2.98836389, 2.63614576, 2.06298576, 1.73999305, 1.4090971 ,
       1.12819288, 0.92043848, 1.20091581, 1.29993016, 1.38187416])}

General structure

def sine(y, t, A, omega, delta):
    dy_dt = A * omega * np.sin(omega * t + delta)
    return dy_dt

def simulate_model(params):
    y0 = params['y0']
    A = params['A']
    omega = params['omega']
    delta = params['delta']
    sol = odeint(sine, y0, time, args=(A, omega, delta))
    return sol.flatten()

Next, we define an error function, this error function, depends on the data and the model predicted outcomes. The optimizer minimizes this error function

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import os
import sys
import scipy.io
from concurrent.futures import ProcessPoolExecutor

# Get path
# Get path to MCMCwithODEs_primer (3 levels up)
project_root = os.path.abspath(os.path.join(os.getcwd(), '..','..','..'))
sys.path.insert(0, project_root)

import sys
sys.path.append('./..')  # or absolute path if needed

from invode import ODEOptimizer, lhs_sample, MSE

Adding constraint

For an example, let’s say we want the value at t = 10, is fixed to 1.5. We can use a constraints.

hyperparam = 0.2
def mse_constrainted(output):
    return np.mean((output - data['y'])**2) + hyperparam*np.abs(output[-1]-1.5)

param_bounds = {
    'y0': 0.91963291, # fixed
    'A': (0.2, 1.5),
    'delta': (-0.5, 0.5),
    'omega': (0.5, 4)
}

time = data['Time']

optimizer_constrained = ODEOptimizer(
    ode_func=simulate_model,
    error_func=mse_constrainted,
    param_bounds=param_bounds,
    seed=42,
    num_top_candidates=2,
    n_samples=300,
    num_iter=10,
    verbose=False,
    verbose_plot=True
)

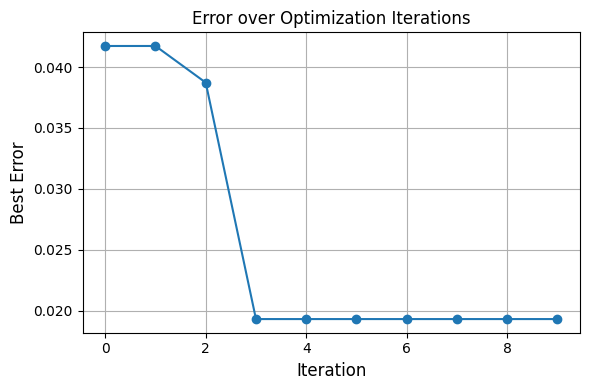
optimizer_constrained.fit()

Fitting Progress: 100%|█████████████████████████████████████████████████| 10/10 [00:01<00:00,  9.97it/s]

Refining params: {'A': 1.1915368305751737, 'delta': -0.02444698040884663, 'omega': 1.985154886052043}
Refining params: {'A': 0.9695259615925091, 'delta': 0.29615770908917377, 'omega': 1.9648598743384087}

({'A': 1.058478997699118,
  'delta': 0.035691140341976554,
  'omega': 1.9916707918835548,
  'y0': 0.91963291},
 0.013854377444252103)

best_params = optimizer_constrained.best_params
best_fit = simulate_model(best_params)



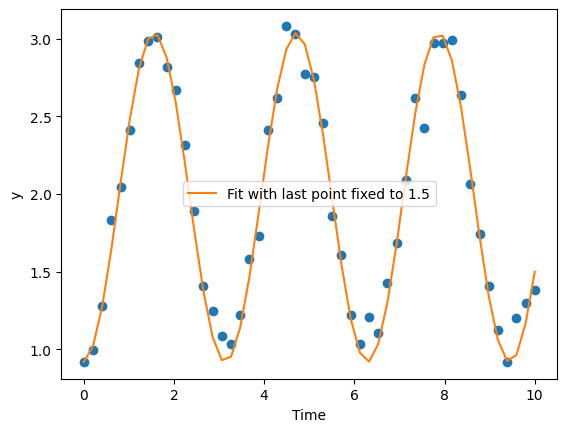
plt.plot(time,data['y'],'o')
plt.plot(time, best_fit, label='Fit with last point fixed to 1.5')
plt.xlabel("Time")
plt.ylabel("y")
plt.legend()

print(f"The last point is {best_fit[-1]}")

The last point is 1.499999984435069